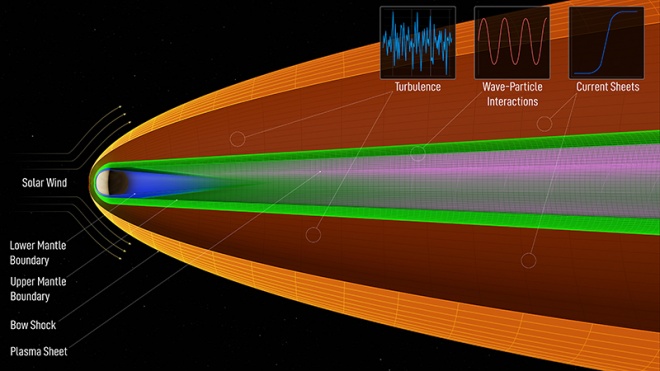
Что находится за пределами нашей Вселенной? Пустота или ещё что-то?
Николай Лобачевский известен тем, что создал новую геометрию, в которой параллельные прямые запросто пересекаются. На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы.






Конечно, параллельные прямые пересекаются. На этом построена вся начертательная геометрия. А на начертательной геометрии построена вся мировая живопись, архитектура, культура в конце концов. Студент, который начертательную геометрию не признает, не признает и культуру тоже, поэтому и аргументация вертится в основном вокруг и. Ну да Бог с ним. Выйдите на улицу и сами убедитесь.








| 89 | Регистрация Вход. Вопросы - лидеры. | |
| 210 | Правила Расширенный поиск. | |
| 363 | Телефон или почта. Интересные факты. | |
| 19 | Обычно называют две гипотезы, и какая из них верна, зависит от геометрии Вселенной. Геометрия может быть плоской или замкнутой. | |
| 466 | Геометрия Лобачевского или гиперболическая геометрия — одна из неевклидовых геометрий , геометрическая теория, основанная на тех же основных аксиомах, что и обычная евклидова геометрия , за исключением аксиомы о параллельных прямых , которая заменяется её отрицанием. Евклидова аксиома о параллельных точнее, одно из эквивалентных ей утверждений, при наличии других аксиом может быть сформулирована следующим образом:. | |
| 100 | В глазах потемнело, когда я услышал: «Исак | |
| 437 | Все сервисы Хабра. | |
| 199 | Для тех, кто хочет вспомнить основы перспективы… В литературе этот парадокс объясняется обычно на примере рельсов, сходящихся к горизонту. Мы тоже не будем нарушать традицию, только разберем этот момент чуть подробнее. | |
| 299 | Параллельные линии не пересекаются. Нигде и никогда. |
Впервые приведена в « Началах » Евклида [ 1 ] :. И если прямая , падающая на две прямые, образует внутренние и по одну сторону углы , меньшие двух прямых , то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых. Евклид использует понятия постулат и аксиома , не объясняя их различия; в разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок.